A couple of months ago, we touched on the subject of aperiodic monotiling. A shape called "the hat" was a breakthrough in the quest to find a single tile shape that would produce a non-repeating pattern. This is often called an einstein, because the German words "ein stein" mean "one tile."
But there is a caveat in the hat, in that it requires both left-handed and right-handed hats. In geometry, that's called reflection. The next quest was to find a monotile shape that did not require reflection in producing a non-repeating pattern.
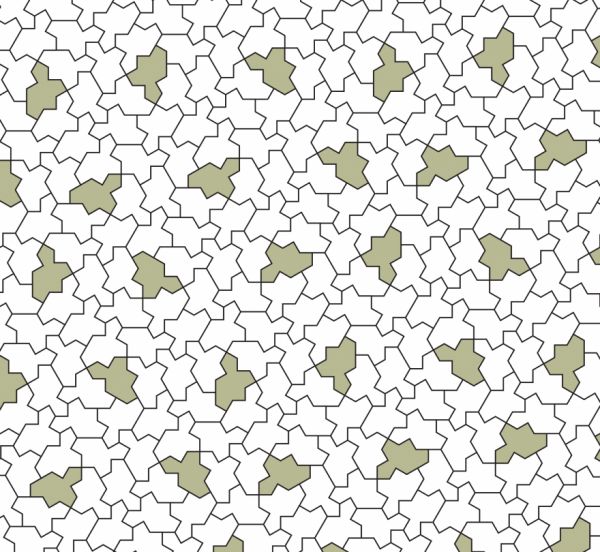
It didn't take long. David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss (the same guys who brought us the hat) present us with "the spectre," a shape that produces a non-repeating pattern and does not require reflection. The term "vampire einstein" comes from the fact that vampires don't produce a reflection in a mirror. But the spectre is real, and makes tiling a bathroom floor in a unique non-repeating manner easier because only one shape needs to milled instead of an unknown proportion of left- and right-handed hats.
The spectre is actually a family of shapes, as the authors have spectre tiles with both straight edges and curved edges. It's a jigsaw puzzle in which all the pieces are the same shape, but you still have to find how they will fit together. -via Metafilter
(Image credit: Smith, Myers, Kaplan, and Goodman-Strauss/CC BY 4.0)